# Wednesday, February 02
:::{.remark}
Extending by zero: for $i: U \embeds X$ an open subspace and $\mcf \in \Sh(U)$, define $i_!\mcf\in \Sh(X)$.
If the target category has a zero object, define this in the sheaf space by extending the zero section:
<!-- Xournal file: /home/zack/SparkleShare/github.com/Notes/Class_Notes/2022/Spring/SheafCohomology/sections/figures/2022-02-02_10-26.xoj -->
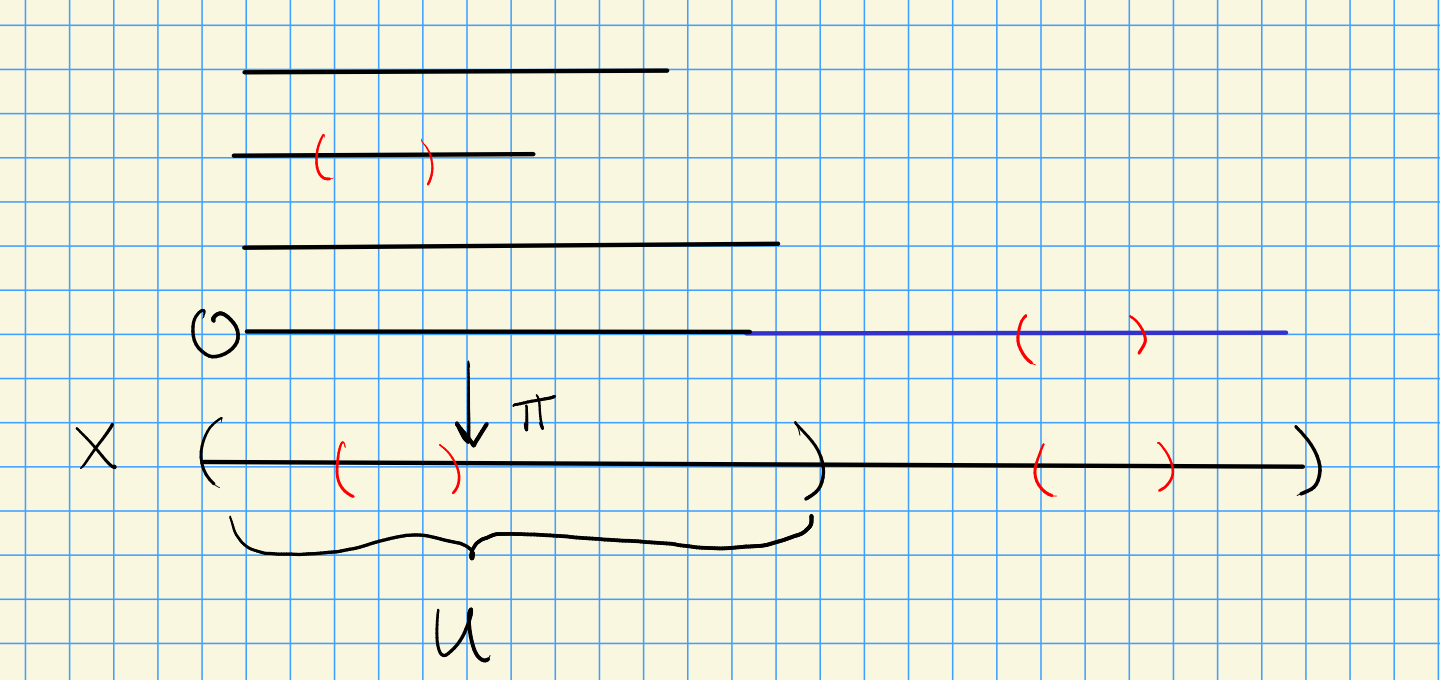
Thus $\Et_{i_! \mcf} = \Et_{\mcf} \disjoint \ts{s_0}$ for $s_0$ the zero section.
:::
:::{.proposition title="?"}
Define a presheaf are given by
\[
(i_! \mcf)^-(V) =
\begin{cases}
F(V) & V \subseteq U
\\
0 & \text{else}.
\end{cases}
.\]
Sheafifying produces an equivalent sheaf, i.e. $(i_! \mcf)^{-+} \cong i_! \mcf$.
:::
:::{.proof title="?"}
Idea: produce a map $(i_! \mcf)^- \to i_! \mcf$ and show it is an isomorphism on stalks.
What are the stalks?
By the sheaf space definition,
\[
(i_! \mcf)_p
=
\begin{cases}
\mcf_p & p\in U
\\
0 & \text{else}.
\end{cases}
.\]
On the other hand, $(i_! \mcf)_p^- = \colim_{V\ni p} \mcf(V)$, but this limit can be taken over the system of open sets $V \subseteq U$, so it yields $\mcf_p$.
:::
:::{.remark}
Consider $X = U \disjoint Z$ with $U$ open and $Z$ closed.
Let $U \injectsvia{i} X$ and $Z\injectsvia{j} X$, and consider $i_* \ro{\mcf}{U}$ and $j_* \ro{\mcf}{U}$.
There is a SES
\[
0 \to i_! \ro{\mcf}{U} \to \mcf \to j_* \ro{\mcf}{Z}\to 0
.\]
:::
:::{.example title="?"}
The sheaf $i_!\ro{\mcf}{U}$ is a subsheaf of $\mcf$, and $j_*\ro{\mcf}{Z}$ is a quotient.
<!-- Xournal file: /home/zack/SparkleShare/github.com/Notes/Class_Notes/2022/Spring/SheafCohomology/sections/figures/2022-02-02_10-46.xoj -->
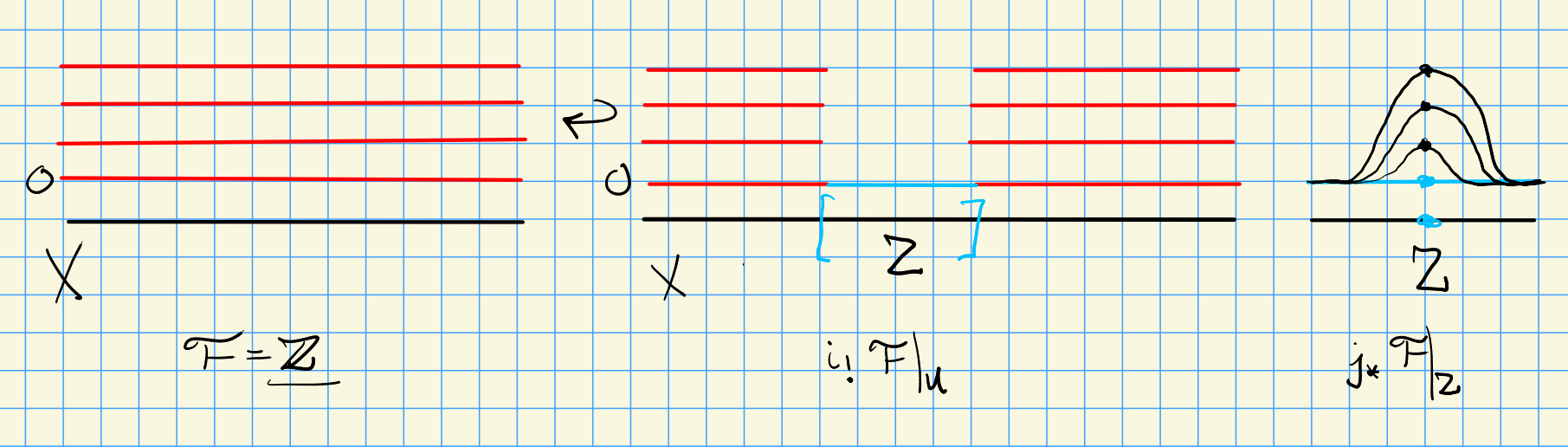
Here $\Et_{\ul{\ZZ}} = \Disjoint_{n\in \ZZ} X$, and $\Et_{j_* \ro{\ul \ZZ}{Z}} X$ glued along $X\sm Z$.
So $i_! \ro{\mcf}{U} \injects \mcf$.
It's important that $Z$ is closed here to get a surjection, since then any point in its complement has a neighborhood $V$ missing $Z$ entirely and $(i_! \mcf)^-(V) = 0$.
Checking the stalks:
| | $\mcf$ | $i_! \ro{\mcf}{U}$ | $j_* \ro{\mcf}{V}$ |
|---------- |---------- |-------------------- |-------------------- |
| $p\in U$ | $\mcf_p$ | $\mcf_p$ | 0 |
| $p\in Z$ | $\mcf_p$ | 0 | $\mcf_p$ |
:::
:::{.example title="?"}
Let $X\in \Alg\Var\slice k$, e.g. $X=\PP^1$, let $Z \subseteq X$ be closed, and let $\mcf \da\OO_X$.
There is a SES $0\to I_Z \to \OO_X\to \OO_Z \to 0$.
:::
:::{.remark}
Note that we have adjunctions
\[
\adjunction{f\inv}{f_*}{\Sh X}{\Sh Y} \\
\adjunction{i_!}{\ro{\wait}{U}}{\Sh ?}{\Sh ?} \\
\adjunction{j_*}{\ro{\wait}{Z} }{\Sh ?}{\Sh ?}
.\]
:::