# Monday, February 28
## Tensors
:::{.remark}
Recall $\modsleft{R} = \modsright{R} = \bimod{R}{R}$ for $R \in \CRing$ associative, but for noncommutative rings these may differ.
- The tensor product is a bifunctor
\[
(\wait)\tensor_R (\wait): \modsright{R} \times \modsleft{R} &\to \Ab\Grp\\
M_R \times _{R}N &\mapsto M_R \tensor_R {}_R N = { F(M\times N) \over (m_1 + m_2) \tensor n - m_1 \tensor n - m_2\tensor n, ma\tensor n - m\tensor an, \cdots}
,\]
satisfying the usual universal property.
- This generalizes:
\[
(\wait)\tensor_R (\wait): \bimods{R}{R} \times \modsleft{R} &\to \modsleft{R}
.\]
- If $\phi\in \CRing(R, S)$, then
\[
(\wait)\tensor_R S: \modsright{R} \to \modsleft{S}
.\]
- This extends to algebras:
\[
(\wait)\tensor_R (\wait): \alg{R}\times \alg{R} \to \alg{R}
,\]
with multiplication given by $(s_1\tensor s_2)\cdot(t_1\tensor t_2) \da (s_1t_1)\tensor (s_2t_2)$.
- There is an adjunction:
\[
[A\tensor_R C, B]_{\rmod} \iso [A, B^C]_{\rmod}
.\]
:::
:::{.corollary title="?"}
Since $A\tensor_R (\wait)$ is a left adjoint, it is right exact.
Thus presentations $R^J\to R^I \to M \to 0$ yield presentations $M^J \to M^I \to M\tensor_R N \to 0$.
:::
:::{.example title="?"}
\[
\CC\tensor_RR \CC \cong \CC \oplus \CC
,\]
writing $\CC = \RR[x]/\gens{x^2+1}$, so
\[
\CC \tensor_\RR { \RR[x] \over \gens{x^2+1}} \cong { \CC[x] \over \gens{x^2+1}} \cong {\CC[x] \over \gens{x-i}} \oplus {\CC[x] \over \gens{x+i}}
.\]
Geometrically, this corresponds to $\colim(\spec \CC\to \spec \RR \from \spec \CC)\cong X\da \spec \CC\tensor_\RR \CC$, where point $\gens{x^2+1}$ splits geometrically and $X\to \spec \RR$ is a 2-to-1 cover over this point.
\begin{tikzcd}
{X\fiberprod{Y}\spec k \cong \spec (S\tensor_R k)} && X && {\AA^{m+n}} &&&& {S=R=k[t_1,\cdots, t_n, x_1,\cdots, x_m]/\gens{q_j(t, x)}} && {k[t_1,\cdots, t_n, x_1,\cdots, x_m]} \\
\\
{\spec k} && Y && {\AA^n \ni \tv{a_1,\cdots, a_n}} &&&& {R=k[t_1,\cdots, t_n]/\gens{p_i(x)}} && {k[t_1,\cdots, t_n]} \\
&&&&&& {} \\
&& {\spec k} &&&&&& k
\arrow[two heads, from=1-11, to=1-9]
\arrow[two heads, from=3-11, to=3-9]
\arrow[hook, from=3-3, to=3-5]
\arrow[hook, from=1-3, to=1-5]
\arrow[from=1-3, to=3-3]
\arrow[from=1-5, to=3-5]
\arrow[from=3-11, to=1-11]
\arrow[from=3-9, to=1-9]
\arrow[from=5-3, to=3-3]
\arrow[from=5-3, to=3-5]
\arrow["{t_i\mapsto a_i}", from=3-11, to=5-9]
\arrow[from=3-1, to=3-3]
\arrow[from=1-1, to=1-3]
\arrow[from=1-1, to=3-1]
\arrow["\lrcorner"{anchor=center, pos=0.125}, draw=none, from=1-1, to=3-3]
\arrow["{p_i(\vector a) = 0, \quad t_i\mapsto a_i}"', from=3-9, to=5-9]
\end{tikzcd}
> [Link to Diagram](https://q.uiver.app/?q=WzAsMTMsWzIsMCwiWCJdLFsyLDIsIlkiXSxbNCwyLCJcXEFBXm4gXFxuaSBcXHR2e2FfMSxcXGNkb3RzLCBhX259Il0sWzgsMiwiUj1rW3RfMSxcXGNkb3RzLCB0X25dL1xcZ2Vuc3twX2koeCl9Il0sWzgsMCwiUz1SPWtbdF8xLFxcY2RvdHMsIHRfbiwgeF8xLFxcY2RvdHMsIHhfbV0vXFxnZW5ze3Ffaih0LCB4KX0iXSxbMTAsMiwia1t0XzEsXFxjZG90cywgdF9uXSJdLFsxMCwwLCJrW3RfMSxcXGNkb3RzLCB0X24sIHhfMSxcXGNkb3RzLCB4X21dIl0sWzQsMCwiXFxBQV57bStufSJdLFsyLDQsIlxcc3BlYyBrIl0sWzgsNCwiayJdLFs2LDNdLFswLDIsIlxcc3BlYyBrIl0sWzAsMCwiWFxcZmliZXJwcm9ke1l9XFxzcGVjIGsgXFxjb25nIFxcc3BlYyAoU1xcdGVuc29yX1IgaykiXSxbNiw0LCIiLDAseyJzdHlsZSI6eyJoZWFkIjp7Im5hbWUiOiJlcGkifX19XSxbNSwzLCIiLDAseyJzdHlsZSI6eyJoZWFkIjp7Im5hbWUiOiJlcGkifX19XSxbMSwyLCIiLDAseyJzdHlsZSI6eyJ0YWlsIjp7Im5hbWUiOiJob29rIiwic2lkZSI6InRvcCJ9fX1dLFswLDcsIiIsMCx7InN0eWxlIjp7InRhaWwiOnsibmFtZSI6Imhvb2siLCJzaWRlIjoidG9wIn19fV0sWzAsMV0sWzcsMl0sWzUsNl0sWzMsNF0sWzgsMV0sWzgsMl0sWzUsOSwidF9pXFxtYXBzdG8gYV9pIl0sWzExLDFdLFsxMiwwXSxbMTIsMTFdLFsxMiwxLCIiLDEseyJzdHlsZSI6eyJuYW1lIjoiY29ybmVyIn19XSxbMyw5LCJwX2koXFx2ZWN0b3IgYSkgPSAwLCBcXHF1YWQgdF9pXFxtYXBzdG8gYV9pIiwyXV0=)
Conclusion:
\[
S\tensor_R k = {k[x_1,\cdots, x_m] \over \gens{q_j(a, x) } }
.\]
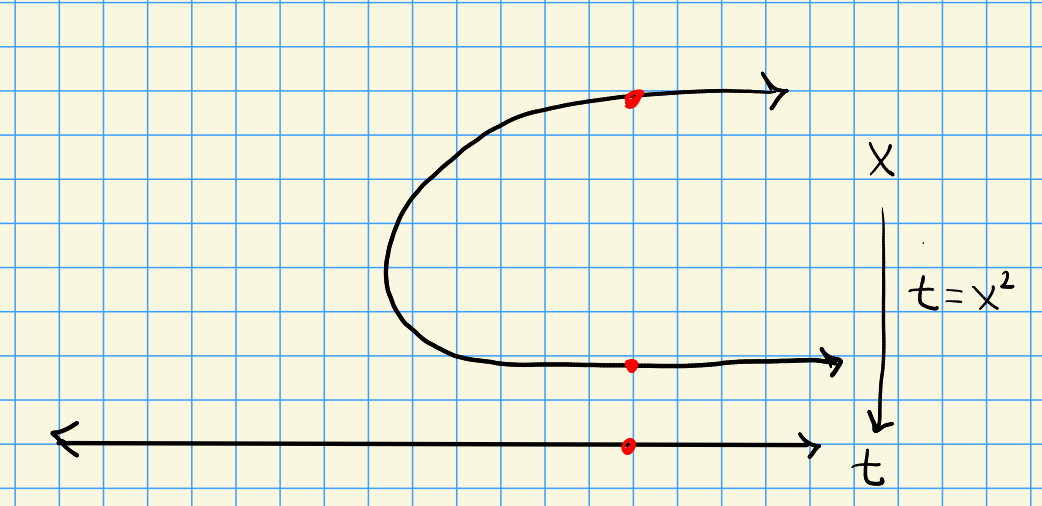
In the previous example, the fiber over $a$ is $\spec k[x]/\gens{x^2-a}$ and the covering map looks like the following:
<!-- Xournal file: /home/zack/SparkleShare/github.com/Notes/Class_Notes/2022/Spring/SheafCohomology/sections/figures/2022-02-28_10-51.xoj -->
:::
:::{.question}
Is direct sum exact as a functor $\cat{A}\cartpower{2}\to \cat A$?
Regard $\cat{A}\cartpower{2} = \cat{A}^{\cat I}$ where $I = \ts{\bullet, \bullet}$ is the discrete 2-object diagram category.
The map $(A_1, A_2)\to A_1 \oplus A_2$ is exact by just summing SESs.
:::
## Cohomology
:::{.remark}
Recall that one can compute $H_*(S^2; \ZZ)$ in several ways.
Method 1: triangulation.
<!-- Xournal file: /home/zack/SparkleShare/github.com/Notes/Class_Notes/2022/Spring/SheafCohomology/sections/figures/2022-02-28_11-01.xoj -->
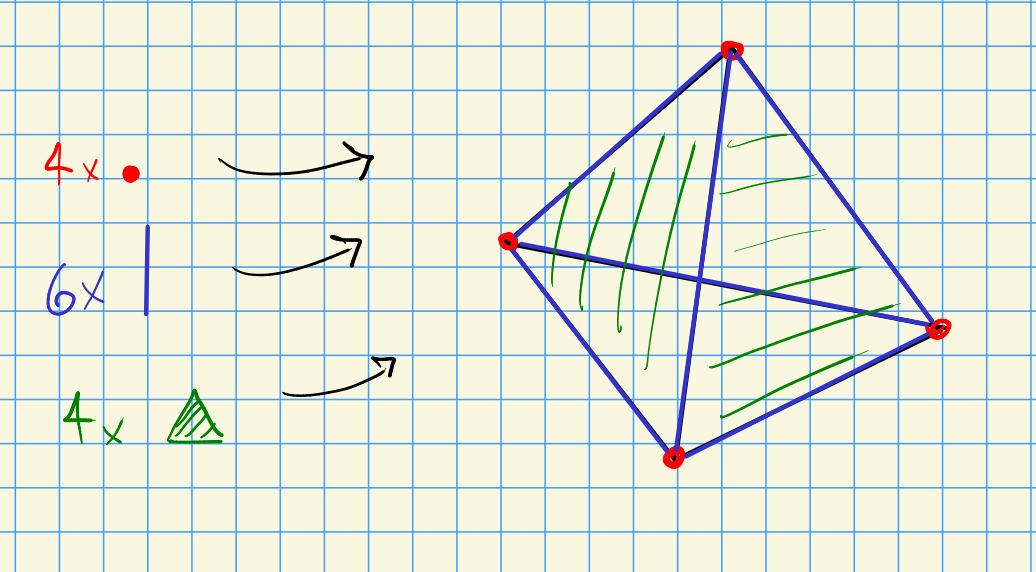
This yields
\[
0 \from \ZZ\cartpower{4} \from \ZZ\cartpower{6}\from \ZZ\cartpower{4} \from 0 \leadsto 0\from \ZZ\from 0 \from \ZZ\from 0
.\]
Method 2: cell complexes.
<!-- Xournal file: /home/zack/SparkleShare/github.com/Notes/Class_Notes/2022/Spring/SheafCohomology/sections/figures/2022-02-28_11-05.xoj -->
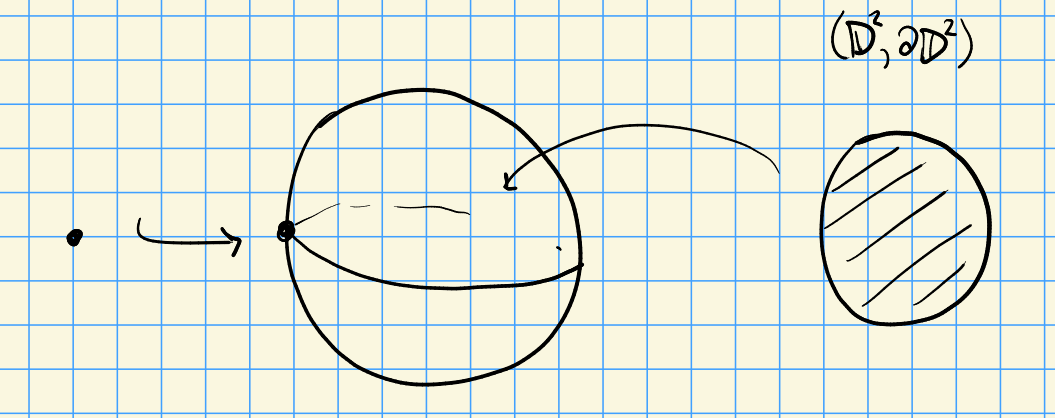
This directly yields
\[
0\from \ZZ\from 0 \from \ZZ \from 0
.\]
:::
:::{.question}
Why are simplices $\Delta_n$ or discs $D^n$ the right things?
:::
:::{.answer}
They are contractible, but more importantly do not themselves have higher homology and are thus *acyclic*.
:::
:::{.remark}
More generally, for $F\in \Ab\Cat(\cat A,\cat B)$, we'll want to resolve by acyclic objects.
Injectives and projectives will be universal such objects, but are often hard to work with, so we'll work on finding more economical acyclic resolutions.
Next time: injectives/projectives and derived functors.
:::