The most current iteration of GOATS can be found at https://dzackgarza.com/GOATS_2020.

Information

This is the website for GOATS, the first in a series of online mini-conferences for graduate students in Geometry and Topology. The speakers will be graduate students, and attendance is open to anyone. We plan to hold these on an ongoing/recurring basis, and will update this page with information about future events.

Conference Poster/Infographic Poster credit: Sarah Blackwell c/o Piktochart

Schedule

Saturday, April 25th, 12:00 PM to 3:30 PM EDT

11:50 AM EDT: Zoom meeting opens

12:00 - 1:00 PM EDT: Noelle Sawyer, Wesleyan University

  • Title: Partial marked length spectrum rigidity (Slides)
  • Abstract: The marked length spectrum of a metric on a compact Riemannian manifold records the length of the shortest closed curve in each free homotopy class. It is known that a negatively curved metric on a compact Riemannian manifold is uniquely determined by its marked length spectrum up to isometry. My results show that under certain conditions on the excluded homotopy classes, a partial marked length spectrum also uniquely determines such a metric.

1:00 - 1:10 PM EDT: Break / Social Event

1:10 - 2:10 PM EDT: Contributed Talks

1:10 - 1:25 PM EDT: Andrew Tawfeek, Amherst College

  • Title: Enumeration of Forman Classes of Discrete Morse Functions
  • Abstract: Discrete Morse Theory, pioneered by Robin Forman around the turn of the century, is an analogue of the classic (Smooth) Morse Theory adapted to mimic the results for CW complexes rather than smooth manifolds. Similar to the smooth case, there is a notion of a gradient of a discrete Morse function on a complex. We focus on the one-dimensional case of graphs and provide a novel approach in counting them, then showcase a beautiful connection between these gradients and the graph Laplacian. Lastly, we introduce the notion of the Morse (simplicial) complex associated to a graph and talk about some interesting future directions to continue research.

1:30 - 1:45 PM EDT: Hannah Turner, University of Texas at Austin

  • Title: Orderability and branched covers of knots (Slides)
  • Abstract: Some groups can be given an ordering which is respected by the group operation. The question of when a 3-manifold group is orderable is intimately related to topological properties of the manifold. Three-manifold groups with a $\mathrm{SL}(2,\mathbb{R})$ representation which has trivial Euler class are orderable. We exploit this fact and techniques of Hu and Tran to determine for any branched cyclic cover of a family of hyperbolic knots, whether its fundamental group is orderable.

1:50 - 2:05 PM EDT: Oğuz Şavk, Bogazici University, Turkey

  • Title: More Brieskorn Spheres Bounding Rational Balls (Slides)
  • Abstract: We call an integral homology sphere non-trivially bounds a rational homology ball if it is obstructed from bounding an integral homology ball. After Fintushel and Stern’s well-known example $\Sigma (2,3,7)$, Akbulut and Larson recently provided the first infinite families of Brieskorn spheres non-trivially bounding rational homology balls: $\Sigma (2,4n+1,12n+5)$ and $\Sigma (3,3n+1,12n+5)$ for odd $n$. Using their technique, we present new such families: $\Sigma (2,4n+3,12n+7)$ and $\Sigma (3,3n+2,12n+7)$ for even $n$.

2:10 - 2:20 PM EDT: Break/Social Event

2:20 - 3:20 PM EDT: Arun Debray, University of Texas at Austin

  • Title: What: Bordism groups. Why: Condensed-matter physics. How: The Adams spectral sequence. (Slides)
  • Abstract: I’ll discuss an application of algebraic topology to theoretical physics: the use of bordism groups to classify symmetry-protected topological (SPT) phases in condensed-matter physics. After introducing both of these concepts, I’ll explain how to use the Adams spectral sequence over A(1) to compute some of these bordism groups. Freed-Hopkins propose a generalization of this bordism-theoretic approach to SPTs in the setting of crystalline phases; in the remaining time, I’ll discuss my work in progress providing supporting evidence for their ansatz.

Participant Information

Adapted from the Knot Online Seminar

To Join the Meeting

  • You will need to download the zoom client and join using the meeting number sent to you via email confirmation after registering.

  • This meeting is open from 11:45am to 3:45pm (EDT).

    • If this is your first time with zoom, we suggest you connect to the meeting room 10 minutes before the start time in order to get used to its functionalities.

  • After you click “join meeting”:

    • You will be directed to the zoom meeting room of GOATS. We encourage you to use your real name as you join. It makes it easier for other participants to communicate with you. You probably want to tick the box join with computer audio, otherwise you won’t be able to hear anything. Both your camera and your microphone will stay off as you join.

    • You will be able to hear and see the speaker, and see their screen/board. You can use the chat to communicate with other participants. Note that you can choose who you send messages to. The speaker will typically not read the chat. To show reaction you may use the non-verbal feed-back buttons at the bottom of the participants window.

Asking Questions

  • If you want to ask a question, you can raise your hand by clicking the “Participants” button:

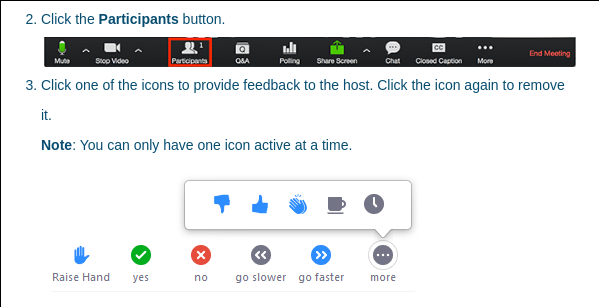
  • At a convenient point, one of the organizers will then inform the speaker that there is a question and give you the ability to unmute yourself. You can then click the “unmute” button and ask your question to the speaker directly.

  • You may also type your questions into chat, which the organizers can then relay to the speaker.

Organizers