The most current iteration of GOATS can be found at https://dzackgarza.com/GOATS_2020.
Information
Submissions for contributed talks are now closed, but will be considering submissions again for a third iteration in the near future. Details will be announced on the main site.
This is the website for GOATS #2, the second in a series of online mini-conferences for graduate students in Geometry and Topology. The speakers will be graduate students, and attendance is open to anyone. We plan to hold these on an ongoing/recurring basis, and will update this page with information about future events.
- You can follow and tweet under the #mathgoats2020 hashtag.
- For those that are interested in speaking at the next GOATS, we welcome you to reach out to any of the organizers directly!
Schedule
Saturday, June 6th, 12:00 PM to 5:30 PM EDT
See also ResearchSeminars.org page.
11:50 AM EDT: Zoom meeting opens
12:00-1:00PM EDT: Marla Williams, University of Nebraska-Lincoln
-
Title: Trisections and Flat Surface Bundles (Slides)
-
Abstract: We’ll start with a look at how to trisect trivial surface bundles over surfaces and how to draw the corresponding diagrams. We’ll then move into a discussion of what changes when we shift to trisecting nontrivial surface bundles, and why flatness matters for my diagram construction.
1:00-1:10 PM EDT: Ten Minute Break
1:10-1:30 PM EDT: Contributed Talk #1, Steve Wheatley, George Mason University
-
Title: Characterizations of $2\dash$Homeomorphic Spaces (Slides)
-
Abstract: In a 2018 paper, Arhangel’skii and Maksyuta give the definition of a $2\dash$homeomorphism, a topological concept that generalizes the notion of a homeomorphism. In this talk, we give some characterizations of spaces that are $2\dash$homeomorphic to spaces possessing various topological properties, including compact spaces and discrete spaces. We also show that, although many topological properties are not preserved under the $2\dash$homeomorphism relation, the property of having finite Cantor-Bendixson height is preserved.
1:30-1:50 PM EDT: Contributed Talk #2, Rhea Palak Bakshi, The George Washington University
-
Title: Framings of Links in 3-manifolds and Torsion in Skein Modules (Slides)
-
Abstract: We show that the only way of changing the framing of a link by ambient isotopy in an oriented $3\dash$manifold is when the manifold admits a properly embedded non-separating $S^2$. This change of framing is given by the Dirac trick, also known as the light bulb trick. The main tool we use is based on McCullough’s work on the mapping class groups of $3\dash$manifolds. We also express our results in the language of skein modules. In particular, we relate our results to the framing skein module and the Kauffman bracket skein module.
1:50-2:10 PM EDT: Break / Social Event #1
Rooms:
- Underrepresented Minorities in Math
- Homotopy Theory
- Set-Theoretic Topology
- Working During COVID (Slides)
2:10-3:10 PM EDT: Duncan Clark, Ohio State University
-
Title: On the Goodwillie Derivatives of the Identity in Structured Ring Spectra (Slides)
-
Abstract: Functor calculus was introduced by Goodwillie as a means for analyzing homotopy functors between suitable model categories. One noteworthy facet is that “nice” functors $F\colon \mathsf{C}\to \mathsf{D}$ are determined by a certain symmetric sequence called the derivatives of $F$.
This sequence of derivatives is known to posses much structure: for instance, the derivatives of the identity functor on the category of based topological spaces is an operad, as first shown by Ching. It is further expected that a result of this type should hold in any suitable model category, and in particular conjectured that the derivatives of the identity on the category of algebras over an operad $\mathcal{O}$ in spectra should be equivalent to $\mathcal{O}$ as operads.
In this talk we produce an intrinsic “homotopy-coherent” operad structure for the derivatives of the identity which is equivalent to that on $\mathcal{O}$, thus resolving the above conjecture. Along the way we will discuss the necessary background of functor calculus and algebras over operads of spectra. Our method is to induce a homotopy coherent operadic pairing on the derivatives by a suitable pairing on the cosimplicial resolution offered by the stabilization adjunction for $\mathcal{O}$-algebras.
Time permitting, we will provide some other applications of our techniques such as a highly homotopy-coherent chain rule for functors of structured ring spectra.
3:10-3:20 PM EDT: Ten Minute Break
3:20-3:40 PM EDT: Contributed Talk #3, Christopher Perez, University of Illinois at Chicago
-
Title: Towers and Elementary Embeddings in Toral Relatively Hyperbolic Groups
-
Abstract: A group $G$ is a tower over a subgroup $H$ if $H$ can be obtained from $G$ via a series of retractions in a nice and very geometric way. In 2011, Chloé Perin proved that if $H$ is an elementarily embedded subgroup of a torsion-free hyperbolic group $G$ (also known as an elementary submodel), then $G$ is a tower over $H$.
The implication of this and similar results is that the geometric structures of certain groups capture their logical structures as well. I will be discussing towers and my recent generalization of Perin’s result to toral relatively hyperbolic groups.
3:40-4:00 PM EDT: Contributed Talk #4, Nikolas Schonsheck, Ohio State University
-
Title: Fibration Theorems for $\mathbf{TQ}\dash$Completion of Structured Ring Spectra
-
Abstract: By considering algebras over an operad $\mathcal{O}$ in one’s preferred category of spectra, we can encode various flavors of algebraic structure (e.g. commutative ring spectra). Drawing intuition from singular homology of spaces and Quillen homology of rings, topological Quillen ($\mathbf{TQ}$) homology is a naturally occurring notion of homology for these objects, with analogies to both singular homology and stabilization of spaces.
For a given $\mathcal{O}\dash$algebra $X$, there is a canonical way (following Bousfield-Kan) to “glue together” iterates $\mathbf{TQ}^n(X)$ of the $\mathbf{TQ}\dash$homology spectrum of $X$ to construct “the part of $X$ that $\mathbf{TQ}\dash$homology sees,” namely its $\mathbf{TQ}\dash$completion. We then ask, “When can $X$ be ‘recovered from’ $\mathbf{TQ}(X)$ in this way?”
Bousfield-Kan consider the analogous question in spaces and conclude that all nilpotent spaces are weakly equivalent to their homology completion. The key technical maneuver of their proof involves showing that certain fibration sequences are preserved by completion. In this talk, we will discuss certain types of fibration sequences of $\mathcal{O}\dash$algebras which are preserved by $\mathbf{TQ}\dash$completion, drawing analogies along the way to the case of pointed spaces.
4:00-4:20 PM EDT: Break / Social Event #2
Rooms:
- Geometric Group Theory
- Homotopy Theory
- Job Search (Academic and Industry)
- Math and #BLM
- Graduate Students with Children
4:20-5:20 PM EDT: Nicholas Cazet, UC Davis
-
Title: Vertex Distortion of Lattice Knots
-
Abstract: The vertex distortion of a lattice knot is the supremum of the ratio of the distance between a pair of vertices along the knot and their distance in the 1-norm. We show analogous results of Gromov, Pardon and Blair-Campisi-Taylor-Tomova about the distortion of smooth knots hold for vertex distortion, the vertex distortion of a lattice knot is 1 only if it is the unknot, and that there are minimal lattice-stick number knot conformations with arbitrarily high distortion.
5:20-5:30 PM EDT: Reception
Participant Information
Adapted from the Knot Online Seminar
To Join the Meeting
-
You will need to download the zoom client and join using the meeting number sent to you via email confirmation after registering.
-
This meeting is open from 11:45am to 3:45pm (EDT).
- If this is your first time with zoom, we suggest you connect to the meeting room 10 minutes before the start time in order to get used to its functionalities.
-
After you click “join meeting”:
-
You will be directed to the zoom meeting room of GOATS. We encourage you to use your real name as you join. It makes it easier for other participants to communicate with you. You probably want to tick the box join with computer audio, otherwise you won’t be able to hear anything. Both your camera and your microphone will stay off as you join.
-
You will be able to hear and see the speaker, and see their screen/board. You can use the chat to communicate with other participants. Note that you can choose who you send messages to. The speaker will typically not read the chat. To show reaction you may use the non-verbal feed-back buttons at the bottom of the participants window.
-
Asking Questions
-
If you want to ask a question, you can raise your hand by clicking the “Participants” button:
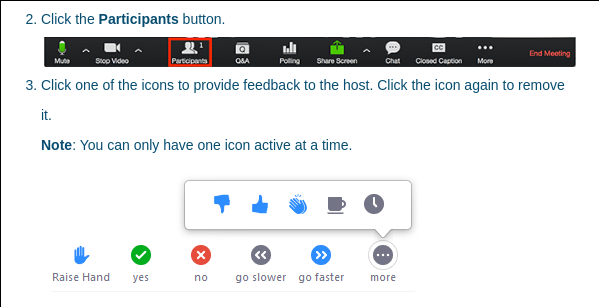
-
At a convenient point, one of the organizers will then inform the speaker that there is a question and give you the ability to unmute yourself. You can then click the “unmute” button and ask your question to the speaker directly.
-
You may also type your questions into chat, which the organizers can then relay to the speaker.
